Kurz SVG – bitmapové efekty (elementární grafické filtry 1.)

V následujícím textu se společně podíváme na základní stavební jednotky bitmapových efektů (filter primitives) podle SVG specifikace. Postupně probereme ty nejzajímavější a nejčastěji používaná primitiva.

Znovu pro pořádek připomínám, že plné znění v nezjednodušené podobě naleznete na webu W3 konzorcia.

Při filtrování RGBA dat může při výpočtech dojít k překročení maximálního rozsahu hodnot. V takovém případě budou hodnoty oříznuty, například záporná hodnota se změní na 0!

Pozn.: Většina filtrů pracuje s takzvanými přednásobenými hodnotami RGB (premultiplied RGB). Míněno přednásobenými hodnotou alfa kanálu (A). Ty, pro které nejsou přednásobené hodnoty výhodné, jako například feColorMatrix a feComponentTransfer, si přednásobené RGB dočasně upraví.

Přehled elementárních grafických filtrů

Dále uvádím seznam základních filtrů, jejichž kombinací lze sestavit libolné grafické efekty. SVG norma tyto elementární stavební kameny nazývá filter primitives. V našem seriálu nebudu detailně probírat všechny. Soustředím se především na údaje důležité pro praktické využití.

• Elementární bitmapové filtry
  • Filter primitive „feBlend“ – prolínání dvou bitmap
  • Filter primitive „feComposite“ – slučování dvou bitmap
  • Filter primitive „feMerge“ – slučování dvou bitmap
  • Filter primitive „feComponentTransfer“ – úpravy jasu
  • Filter primitive „feColorMatrix“ – úpravy barevnosti
  • Filter primitive „feConvolveMatrix“ – kombinování sousedních bodů
  • Filter primitive „feFlood“ – vyplnění plochy
  • Filter primitive „feImage“ – vložení další grafiky
  • Filter primitive „feOffset“ – posuv
  • Filter primitive „feDisplacementMap“ – deformace
  • Filter primitive „feTile“ – vyplnění vzorkem
  • Filter primitive „feGaussianBlur“ – rozostření
  • Filter primitive „feMorphology“ – nasílení / zúžení
  • Filter primitive „feTurbulence“ – generování šumu
  • Filter primitive „feSpecularLighting“ – osvětlovací efekt
  • Filter primitive „feDiffuseLighting“ – osvětlovací efekt
• Definice světelných zdrojů (viz Kurz SVG – bitmapové efekty (definice W3C, parametry osvětlení))
  • Light source „feDistantLight“ – vzdálený zdroj světla
  • Light source „fePointLight“ – bodové světlo
  • Light source „feSpotLight“ – reflektor

Společné atributy

• x, y, width, height – pomocí těchto nepovinných parametrů lze zúžit oblast pro výpočet konkrétního elementárního filtru
• in – určuje vstup filtru; možné hodnoty (viz též dále): SourceGraphic, SourceAlpha, BackgroundImage, BackgroundAlpha, FillPaint, StrokePaint nebo název obrazové proměnné definované pomocí atributu result v nějakém předcházejícím filtru; pokud tento nepovinný atribut není uveden, použije se výstup bezprostředně předcházející operace (v případě první operace v bloku filter se logicky použije původní grafika = SourceGraphic)
• result – výsledek operace může být na tomto místě pojmenován (nabízím vám programátorskou analogii – představte si to, jako by byl výsledek filtrování uložen do obrazové proměnné s uvedeným jménem); pokud tento atribut není v SVG kódu uveden, je výsledek dané operace ihned předán jako implicitní vstup dalšímu zapsanému filtru

Definice klíčových slov

• SourceGraphic – udává, že vstupem filtrovací operace je původní RGBA grafika (tedy ta skupina, na kterou aplikujeme filtrování) po vykreslení vektorů a případných rastrových obrázků (ale před jakoukoli operací filtrování)
• SourceAlpha – pouze alfa kanál (tedy průhlednost) původní zdrojové grafiky – viz předchozí bod
• BackgroundImage – obraz pozadí, viz „Přístup k obrazu pozadí“ v článku Kurz SVG – bitmapové efekty (definice W3C, parametry osvětlení)
• BackgroundAlpha – průhlednost pozadí, viz „Přístup k obrazu pozadí“ v článku Kurz SVG – bitmapové efekty (definice W3C, parametry osvětlení)
• FillPaint – výplň zdrojové grafiky; plocha FillPaint je kompletně neprůhledná (pokud výplň samotná nemá nastavenu průhlednost pomocí atributu fill-opacity)
• StrokePaint – výplň tahů (obrysů) zdrojové grafiky

Podrobný popis filtrovacích elementů

Následující část obsahuje podrobný popis filtrovacích elementů z normy SVG. Díky silné praktické orientaci si dovoluji tvrdit, že je tento text také daleko přehlednější a použitelnější než originální informace organizace W3C.

Snažím se dále čtenářům předložit u každého jednotlivého grafického filtru názorný příklad, který by co nejlépe osvětlil funkčnost efektu a význam jednotlivých parametrů. Na rozdíl od originální specifikace také nejsou jednotlivá primitiva řazena abecedně, nýbrž jsou seskupena podle podobné funkčnosti.

Pozn.: Mnoho grafických ukázek vychází z kódů uvedených ve specifikaci SVG – ovšem dost často jsem tyto příklady modifikoval tak, aby byly buď názornější a pochopitelnější, nebo vizuálně přitažlivější…

Filter primitive „feBlend“

Filtr slučuje dvě různé bitmapy do jedné pomocí prolínacích režimů dobře známých např. z Photoshopu. Na tomto místě platí více než kde jinde výrok „jeden obraz řekne více než tisíc slov“:

Demonstrace režimů prolínání – podívejte se, jak dopadne vykreslení v konkrétním režimu postupně na černé-bílé-(červené) barvě – 50% šedé (originální SVG, cca 1 kB)

Atributy:

• mode – režim prolínání, možné hodnoty: normal, multiply, screen, darken, lighten
• in2 – druhá vstupní bitmapa, význam je obdobou výše zmiňovaného atributu in

Matematické vyjádření slučování obrazů:

Pozn.: Připomínám, že se zde operuje s přednásobenými hodnotami RGB (premultiplied RGB) – míněno přednásobenými hodnotou alfa kanálu (A).

• význam proměnných:
  • qr – průhlednost výsledku
  • cr – výsledná barva (RGB) – přednásobená
  • qa – průhlednost obr. A
  • qb – průhlednost obr. B
  • ca – barva obr. A – přednásobená
  • cb – barva obr. B – přednásobená
• průhlednost pixelů ve výsledku:
  • qr = 1 – (1-qa)*(1-qb)
• vzorce pro jednotlivé režimy:
  • normal: cr = (1-qa)*cb + ca
  • multiply: cr = (1-qa)*cb + (1-qb)*ca + ca*cb
  • screen: cr = cb + ca – ca * cb
  • darken: cr = Min ((1-qa)*cb + ca, (1-qb)*ca + cb)
  • lighten: cr = Max ((1-qa)*cb + ca, (1-qb)*ca + cb)

Režim normal odpovídá standardní metodě slučování v SVG – viz Simple alpha compositing.

Pokud se podíváte na zdrojový kód filtrů v tomto příkladu, uvidíte, že filtrovaný objekt je slučován přímo s podkladem. Jejich aplikací na libovolný prvek SVG grafiky proto získáte obdobu čtyř nejzákladnějších režimů prolínání vrstev. (Ty jsou známé původně z Photoshopu a nyní dostupné i v Illustratoru 9+ a InDesignu 2+.)

Pozn.: ASV obsahuje jako nestandardní rozšíření všechny prolínací režimy na úrovni Illustratoru 9 a InDesignu 2. (Aplikují se na libovolný objekt zápisem atributu a:adobe-blending-mode="overlay" ve jmenném prostoru XML xmlns:a= "http://ns.adobe.com/AdobeSVGViewerExtensions/3.0/".) Jakožto nestandardní je ovšem nelze příliš doporučovat.

Illustrator: Režimy prolínání v profesionální praxi

Filter primitive „feComposite“

Filtr ve výsledku kombinuje dvě vstupní bitmapy podle algoritmu Porter-Duff. Možné operace přitom jsou: over, in, atop, out, xor. Jejich význam nejlépe demonstruje vizuální příklad:

V této ukázce se postupně v různých režimech přes modrý trojúhelník kreslí zrcadlově převrácený červený trojúhelník. Upozornit mohu mimo jiné na fakt, že operace „in“ je v podstatě maskování (maskou je přitom zmíněný modrý trojúhelník), „out“ je rovněž maskovací operace, ale s inverzí masky (originální SVG, cca 1 kB)

A jak to vypadá v XML?

<filter id=“in“ filterUnits=“objectBoundingBox“
  x=“-5%“ y=“-5%“ width=“110%“ height=“110%“>
  <feFlood flood-color=“#ffffff“ flood-opacity=“1″ result=“flood“/>
  <feComposite in=“SourceGraphic“ in2=“BackgroundImage“
    operator=“in“ result=“comp“/>
  <feMerge> <feMergeNode in=“flood“/> <feMergeNode in=“comp“/> </feMerge>
</filter>

Dále je možná takzvaná aritmetická operace, užitečná například při kombinování výsledků feDiffuseLighting a feSpecularLighting s nějakou texturou.

Matematický zápis aritmetické operace:

• výsledek = k1*i1*i2 + k2*i1 + k3*i2 + k4

Atributy:

• operator – možné hodnoty: over, in, out, atop, xor, arithmetic
• k1, k2, k3, k4 – konstanty pro výpočet, pokud je operator=“arithmetic“, jejich výchozí hodnota je vždy 0
• in2 – definuje druhou vstupní bitmapu

Filter primitive „feMerge“

Jednoduše řečeno provádí tento filtr totéž co feComposite v režimu „over“, jenomže pro libovolný počet bitmapových vrstev. Obecně to bude vypadat takto:

<feMerge>
  <feMergeNode in=“bitmapa1″/>
  <feMergeNode in=“bitmapa2″/>
  <feMergeNode in=“…“/>
…
</feMerge>

Na uvedeném výpisu názorně vidíte, jak zapsat vícero vnořených prvků feMergeNode jejichž atributy in definují jednotlivé slučované vrstvy.

Filter primitive „feComponentTransfer“

Tento filtr přepočítává RGBA data podle následujícího schematu:

• R‘ = feFuncR( R )
• G‘ = feFuncG( G )
• B‘ = feFuncB( B )
• A‘ = feFuncA( A )

Nabízí se k použití pro dobře známé operace typu úprava jasu, kontrastu a podobně. Na rozdíl od většiny pracuje s nepřednásobenými hodnotami RGB.

Demonstrace funkce filtru (originální SVG, cca 1 kB)

Všední úkaz z monitoru grafika…

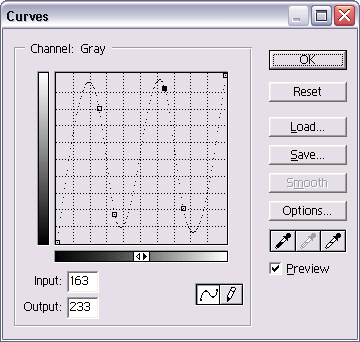
Photoshop: Křivky slouží primárně pro úpravu jasu a kontrastu, ale jejich kreativním využitím se lze dostat do netušených oblastí…

Podle typu zvolené operace v atributu type bude přirozeně nutné přidat další atributy s parametry:

1. Pro funkci identity:
   C‘ = C
   (C zde samozřejmě zastupuje kompozitní barvu)
2. Pro funkci table: Lineární interpolace podle tabulkových hodnot uvedených v atributu tableValues.
   Interpolační vzorec je definován následujícím způsobem. Tabulka obsahuje (N+1) hodnot. Pro hodnotu C z k-tého intervalu tabulky vypočteme výslednou barvu C‘ takto:
   C‘ = table_k + (C-k/N)*(table_k+1-table_k)
   (vzorec předpokládá hodnoty barev C v rozsahu 0..1 a indexu k v rozsahu 0..N)
3. Pro funkci discrete: Vše je v podstatě shodné s operací table, pouze nedojde k interpolaci:
   C‘ = table_k
4. Pro funkci linear je výpočet následující:
   C‘ = slope * C + intercept
5. Pro funkci gamma je to exponenciála:
   C‘ = amplitude * pow(C, exponent) + offset
   (pow = mocnina)

Atributy:

• type – typ funkce, možné hodnoty: identity, table, discrete, linear, gamma; podle typu vybrané funkce budou potřeba některé z následujících atributů
• tableValues – seznam hodnot oddělených mezerami nebo čárkami
• slope – strmost přímky, výchozí hodnota se rovná 1
• intercept – posun přímky na svislé ose funkce
• amplitude – amplituda gama funkce, výchozí hodnota 1
• exponent – exponent gama funkce, výchozí hodnota 1
• offset – „svislý“ posun gama funkce

Nyní už vám pochopení ukázkového SVG kódu jistě nebude činit problémy:

<?xml version=“1.0″?>
<!DOCTYPE svg PUBLIC „-//W3C//DTD SVG 1.1//EN“
          „http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd“>
<svg width=“320px“ viewBox=“0 0 800 440″
     xmlns=“http://www.w3.org/2000/svg“ version=“1.1″>
  <title>
  feComponentTransfer – operace s tabulkou barev – www.interval.cz
  </title>
  <desc>
  Pomoci tohoto filtru muzete realizovat operace ktere jsou
  ve Photoshopu k nalezeni pod nabidkou „Image/Adjust/Levels“
  resp. „Curves“.
  </desc>
  <defs>
    <linearGradient id=“MyGradient“ gradientUnits=“userSpaceOnUse“
      x1=“100″ y1=“0″ x2=“600″ y2=“0″>
      <stop offset=“0″ stop-color=“#ff0000″ />
      <stop offset=“.33″ stop-color=“#00ff00″ />
      <stop offset=“.67″ stop-color=“#0000ff“ />
      <stop offset=“1″ stop-color=“#000000″ />
    </linearGradient>
    <filter id=“Identity“ filterUnits=“objectBoundingBox“
            x=“0%“ y=“0%“ width=“100%“ height=“100%“>
      <feComponentTransfer>
        <feFuncR type=“identity“/>
        <feFuncG type=“identity“/>
        <feFuncB type=“identity“/>
        <feFuncA type=“identity“/>
      </feComponentTransfer>
    </filter>
    <filter id=“Table“ filterUnits=“objectBoundingBox“
            x=“0%“ y=“0%“ width=“100%“ height=“100%“>
      <feComponentTransfer>
        <feFuncR type=“table“ tableValues=“0 0 1 1″/>
        <feFuncG type=“table“ tableValues=“1 1 0 0″/>
        <feFuncB type=“table“ tableValues=“0 1 1 0″/>
      </feComponentTransfer>
    </filter>
    <filter id=“Linear“ filterUnits=“objectBoundingBox“
            x=“0%“ y=“0%“ width=“100%“ height=“100%“>
      <feComponentTransfer>
        <feFuncR type=“linear“ slope=“.5″ intercept=“.25″/>
        <feFuncG type=“linear“ slope=“.5″ intercept=“0″/>
        <feFuncB type=“linear“ slope=“.5″ intercept=“.5″/>
      </feComponentTransfer>
    </filter>
    <filter id=“Gamma“ filterUnits=“objectBoundingBox“
            x=“0%“ y=“0%“ width=“100%“ height=“100%“>
      <feComponentTransfer>
        <feFuncR type=“gamma“ amplitude=“2″ exponent=“5″ offset=“0″/>
        <feFuncG type=“gamma“ amplitude=“2″ exponent=“3″ offset=“0″/>
        <feFuncB type=“gamma“ amplitude=“2″ exponent=“1″ offset=“0″/>
      </feComponentTransfer>
    </filter>
  </defs>
  <g font-family=“Verdana“ font-size=“75″
     font-weight=“bold“ fill=“url(#MyGradient)“ >
    <rect x=“100″ y=“0″ width=“600″ height=“20″ />
    <text x=“100″ y=“90″ filter=“url(#Identity)“>Identity</text>
    <text x=“100″ y=“190″ filter=“url(#Table)“ >TableLookup</text>
    <rect x=“100″ y=“190″ width=“600″ height=“20″ filter=“url(#Table)“ />
    <text x=“100″ y=“290″ filter=“url(#Linear)“ >LinearFunc</text>
    <rect x=“100″ y=“290″ width=“600″ height=“20″ filter=“url(#Linear)“ />
    <text x=“100″ y=“390″ filter=“url(#Gamma)“ >GammaFunc</text>
    <rect x=“100″ y=“390″ width=“600″ height=“20″ filter=“url(#Gamma)“ />
  </g>
  <rect fill=“none“ stroke=“blue“ x=“1″ y=“1″ width=“798″ height=“438″/>
</svg>

Filter primitive „feColorMatrix“

Pomocí níže uvedené matematické maticové operace se realizují všem grafikům jistě důvěrně známé operace typu změna saturace barev nebo třeba posuv barevného spektra…

Matice pro výpočet zobrazení filtru feComponentTransfer‘

Při výpočtu se tentokráte pracuje s nepřednásobenými hodnotami barev.

Možná je i extrakce jednotlivých barvových kanálů (viz poslední dva řádky) (originální SVG, cca 1 kB)

A tohle jistě znáte z praxe…

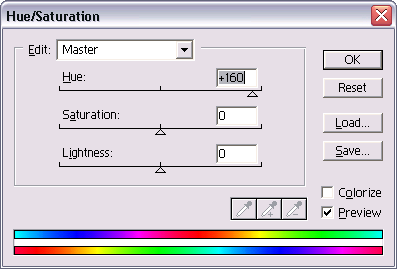
Photoshop: Úpravy sytosti barev a posuv barevného spektra

Atributy:

• type – uvádí typ operace: matrix (zcela obecný výpočet, kdy je nutno udat všech 5×4 hodnot výpočetní matice), saturate (změna saturace neboli sytosti barev), hueRotate (posuv barevného spektra), luminanceToAlpha (hodnota průhlednosti je odvozena z jasu příslušného bodu)
• values – atribut obsahuje seznam hodnot nutných pro příslušný typ výpočtu:
  • pro „matrix“ – všech 5×4 hodnot matice (a00 a01 a02 a03 a04 a10 a11 … a34)
  • pro „saturate“ – jedno reálné číslo v rozsahu 0…1
  • pro „hueRotate“ – jedno reálné číslo (úhlové stupně)
  • pro „luminanceToAlpha“ – není potřeba žádná hodnota

XML kód ukázky:

<?xml version=“1.0″?>
<!DOCTYPE svg PUBLIC „-//W3C//DTD SVG 1.1//EN“
          „http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd“>
<svg width=“320px“ viewBox=“0 0 800 640″
     xmlns=“http://www.w3.org/2000/svg“ version=“1.1″>
  <title>
  feColorMatrix – priklady barvove korekce – www.interval.cz
  </title>
  <desc>
  Pomoci tohoto filtru muzete realizovat operace ktere jsou
  ve Photoshopu k nalezeni pod nabidkou „Image/Adjust/Hue/Saturation“.
  Posledni 2 priklady ukazuji dalsi mozne vyuziti obecne matice –
  extrakce jednotlivych barvovych kanalu.
  </desc>
  <defs>
    <linearGradient id=“MyGradient“ gradientUnits=“userSpaceOnUse“
      x1=“100″ y1=“0″ x2=“500″ y2=“0″>
      <stop offset=“0″ stop-color=“#f00″ />
      <stop offset=“.33″ stop-color=“#0f0″ />
      <stop offset=“.67″ stop-color=“#00f“ />
      <stop offset=“1″ stop-color=“#000″ />
    </linearGradient>
    <filter id=“MatrixRed“ filterUnits=“objectBoundingBox“
            x=“0%“ y=“0%“ width=“100%“ height=“100%“>
      <feColorMatrix type=“matrix“ in=“SourceGraphic“
           values=“.99 .00 .00 0 0
                   .00 .00 .00 0 0
                   .00 .00 .00 0 0                   
.00 .00 .00 1 0″/>
    </filter>
    <filter id=“MatrixGreen“ filterUnits=“objectBoundingBox“
            x=“0%“ y=“0%“ width=“100%“ height=“100%“>
      <feColorMatrix type=“matrix“ in=“SourceGraphic“
           values=“.00 .00 .00 0 0
                   .00 .99 .00 0 0
                   .00 .00 .00 0 0                   
.00 .00 .00 1 0″/>
    </filter>
    <filter id=“Saturate“ filterUnits=“objectBoundingBox“
            x=“0%“ y=“0%“ width=“100%“ height=“100%“>
      <feColorMatrix type=“saturate“ in=“SourceGraphic“ values=“30%“/>
    </filter>
    <filter id=“HueRotate90″ filterUnits=“objectBoundingBox“
            x=“0%“ y=“0%“ width=“100%“ height=“100%“>
      <feColorMatrix type=“hueRotate“ in=“SourceGraphic“ values=“90″/>
    </filter>
    <filter id=“LuminanceToAlpha“ filterUnits=“objectBoundingBox“
            x=“0%“ y=“0%“ width=“100%“ height=“100%“>
      <feColorMatrix type=“luminanceToAlpha“ in=“SourceGraphic“/>
     </filter>
  </defs>
  <rect fill=“none“ stroke=“blue“
        x=“1″ y=“1″ width=“798″ height=“638″/>
  <g font-family=“Verdana“ font-size=“75″
     font-weight=“bold“ fill=“url(#MyGradient)“ >
    <rect x=“100″ y=“0″ width=“500″ height=“20″ />
    <text x=“100″ y=“90″>Unfiltered</text>
    <text x=“100″ y=“190″ filter=“url(#Saturate)“ >Saturate</text>
    <rect x=“100″ y=“190″ width=“500″ height=“20″ filter=“url(#Saturate)“ />
    <text x=“100″ y=“290″ filter=“url(#HueRotate90)“ >HueRotate</text>
    <rect x=“100″ y=“290″ width=“500″ height=“20″ filter=“url(#HueRotate90)“ />
    <text x=“100″ y=“390″ filter=“url(#LuminanceToAlpha)“ >Luminance</text>
    <rect x=“100″ y=“390″ width=“500″ height=“20″ filter=“url(#LuminanceToAlpha)“ />
    <text x=“100″ y=“490″ filter=“url(#MatrixRed)“ >R-channel</text>
    <rect x=“100″ y=“490″ width=“500″ height=“20″ filter=“url(#MatrixRed)“ />
    <text x=“100″ y=“590″ filter=“url(#MatrixGreen)“ >G-channel</text>
    <rect x=“100″ y=“590″ width=“500″ height=“20″ filter=“url(#MatrixGreen)“ />
  </g>
</svg>

Filter primitive „feConvolveMatrix“

Pohybové rozostření (originální SVG, cca 1 KB)

Pro dosažení výsledku tento filtr navzájem kombinuje sousedící obrazové body. Mezi efekty, kterých lze dosáhnout tímto postupem, patří například rozostření a zostření, detekce hran (blurring či sharpening, edge detection, embossing, beveling) a další.

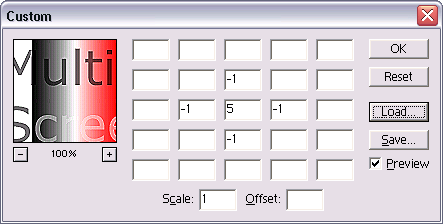
Ekvivalent SVG filtru feConvolveMatrix ve Photoshopu. Jedná se o jednu ze základních operací bitmapové grafiky na níž je postavena spousta dalších komplexnějších efektů.

Filtr lze matematicky popsat jako aplikaci konvoluční matice na zdrojovou bitmapu. Toto je schematický zápis příslušného algoritmu:

VÝSTUP_X,Y = (
   SUMA(I=0 to [orderY-1]) {
      SUMA(J=0 to [orderX-1]) {
         in_{X-targetX+J, Y-targetY+I}
         * kernelMatrix_{orderX-J-1, orderY-I-1}
      }
   }
) / divisor + bias

Atributy:

• order – rozměr konvoluční matice, volitelně lze uvést i druhou hodnotu – pokud matice není čtvercová
• kernelMatrix – vlastní obsah konvoluční matice (kernelu) zapsán po řádcích
• divisor – dělitel je součtem všech členů matice a je nepovinný (součet bude prohlížečem SVG grafiky doplněn automaticky; pro případ, kdy by byl roven 0, bude změněn na hodnotu 1)
• bias – konstanta, která se přičte k výsledné hodnotě (výhodná může být např. v když je třeba aby prázdný (nulový) výstup byl 50% šedá barva)
• targetX – je (nepovinná) relativní X poloha konvoluční matice vůči pixlu, pro který zrovna probíhá výpočet; sloupec matice umístěný co nejvíce vlevo má číslo 0; výchozí hodnotou atributu je umístění matice na střed
• targetY – je (nepovinná) relativní Y poloha konvoluční matice vůči pixlu, pro který zrovna probíhá výpočet; nejhořejší sloupec matice má číslo 0; výchozí hodnotou atributu je umístění matice na střed
• edgeMode – určuje způsob výpočtu na okrajích obr. rastru, kde samozřejmě některé obrazové body nutné pro výpočet neexistují; možné hodnoty s významem uvedeným v závorkách jsou: duplicate (zopakují se okrajové body), wrap (vezmou se hodnoty z opačného okraje bitmapy – možná ještě lepší je představit si, jako by se k hraně, kde nám chybí pixly přidala ještě jedna kopie obrazového rastru – podobně jako se skládají vedle sebe dlaždice) a none (použijí se nulové – černé hodnoty)
• kernelUnitLength – aby byla zajištěna škálovatelnost a nezávislost filtru na rozlišení, je dobré zde nastavit, jak velká je vlastně jedna buňka matice; lze uvést jednu nebo dvě hodnoty (pokud se měřítko ve směru Y liší); jestliže hodnotu nezapíšete, SVG prohlížeč předpokládá, že jedna buňka konvoluční matice odpovídá jednomu pixlu obrázku, což je možná rychlejší na výpočet, ale výsledek se bude lišit podle rozlišení výstupního zařízení
• preserveAlpha – pokud se nastaví na hodnotu „true“ bude zachován kanál průhlednosti, výchozí hodnota „false“ způsobí aplikaci filtru na všechny čtyři obrazové kanály

SVG kód příkladu následuje:

<?xml version=“1.0″?>
<!DOCTYPE svg PUBLIC „-//W3C//DTD SVG 1.1//EN“
          „http://www.w3.org/Graphics/SVG/1.1/DTD/svg11.dtd“>
<svg width=“320px“ viewBox=“0 0 320 120″
     xmlns=“http://www.w3.org/2000/svg“
     xmlns:xlink=“http://www.w3.org/1999/xlink“>
  <title>feConvolveMatrix – www.interval.cz</title>
  <desc>
  Mimo to, ze se zde demonstruje funkcnost vyse uvedeneho
  filtru, upozornuji na CHYBEJICI atribut „kernelUnitLength“.
  Pokud jej neuvedete, bude vypocet fitru rychlejsi, ale
  relativni velikost efektu se bude menit v zavislosti
  na meritku zobrazeni. (Vyzkousejte „ZOOM“ v SVG prohlizeci!)
  </desc>
  <defs>
    <filter id=“motionBlur“ filterUnits=“objectBoundingBox“
      x=“0%“ y=“-3%“ width=“120%“ height=“106%“>
      <feConvolveMatrix in=“SourceGraphic“ edgeMode=“wrap“
        order=“11,1″ kernelMatrix=“0.2 0.5 1 2 3 4 5 6 7 8 22″/>
    </filter>
  </defs>
  <rect fill=“white“ stroke=“blue“ x=“1″ y=“1″ width=“318″ height=“118″/>
  <text x=“20″ y=“32″ font-size=“36px“ filter=“url(#motionBlur)“>
    feConvolveMatrix
  </text>
  <image xlink:href=“svg.gif“
    x=“20″ y=“40″ width=“80″ height=“31″/>
  <image xlink:href=“svg.gif“
    x=“20″ y=“80″ width=“80″ height=“31″ filter=“url(#motionBlur)“/>
</svg>

Starší komentáře ke článku

Pokud máte zájem o starší komentáře k tomuto článku, naleznete je zde.