Java a 3D grafika – Geometry (normálové vektory)

Objekty, které jsme vytvořili v předchozím článku, nebylo možno osvětlovat. V tomto článku tento nedostatek napravíme a naučíme se pracovat s normálovými vektory, které jsou pro osvětlování nezbytné.

Jako normálové vektory označujeme v počítačové grafice vektory, které jsou kolmé na povrch tělesa a mají jednotkovou velikost. Jako takové jsou normálové vektory zcela nepostradatelné pro osvětlování, protože nám dávají informaci o úhlu, který v daném bodě svírá dopadající paprsek s povrchem. (Jediná složka světla, která by sama o sobě normálové vektory nepotřebovala, je ambientní složka, ale ta nevytváří plastický obraz.)

Normálové vektory počítáme pro každý vrchol tělesa zvlášť. Pokud jsou vektory ve všech vrcholech jednoho trojúhelníku stejné a vektory určující směr světla v těchto vrcholech jsou rovněž stejné, pak má daný trojúhelník po celé své ploše konstantní barvu. Pokud jsou ale tyto vektory různé a máme zapnuté Gouraudovo stínování, mění se barva trojúhelníku po jeho ploše, čímž můžeme dosáhnout dojmu oblých tvarů, přestože ve skutečnosti jsou naše tělesa vytvořena z jednotlivých trojúhelníků. Nejlépe je to ilustrováno na příkladu kvádru a koule.

U těles, kde chceme, aby byla zachována jejich „hranatost“, máme práci o něco jednodušší než u těles oblých, jak ostatně sami uvidíte. Stačí nám pouze spočítat normálové vektory pomocí vektorového součinu vektorů daných vrcholy daného trojúhelníku a operace normalizace. Při využití tohoto postupu nicméně musíme mít stále na zřeteli, že směr vektoru získaného pomocí vektorového součinu závisí na pořadí v jakém vektory násobíme, a že by se nám tedy snadno mohlo stát, že by některé trojúhelníky nebyly vidět, pokud by jejich normálové vektory byly orientovány na špatnou stranu.

Tyto trojúhelníky by nemusely být vidět dokonce ani, kdybychom je nechtěli osvětlovat a nepočítali bychom jejich normálové vektory, protože zadní strany nemusí být kvůli zvýšení výkonu renderovány (jak renderovat i zadní strany si ukážeme dále). A která strana je přední a která zadní se určuje právě pomocí normálových vektorů.

Výpočet normálového vektoru je pro přehlednost zobrazen na dalším obrázku.

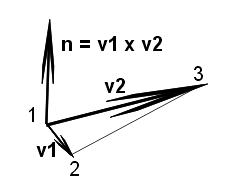
Správnou orientaci normálových vektorů lze zajistit tak, že budeme vrcholy zadávat za sebou, aby když se díváme zpředu na viditelnou stranu trojúhelníku, byly zadané vrcholy orientovány proti směru chodu hodinových ručiček (kvůli pravidlu pravé ruky).

Pokud však chceme, aby u našeho tělesa byly vidět i zadní strany trojúhelníků, musíme udělat ještě něco navíc – jednak v objektu PolygonAttributes zapnout zobrazování zadních stran pomocí následujícího kódu…

PolygonAttributes polygonAttributes = new PolygonAttributes();
polygonAttributes.setCullFace(PolygonAttributes.CULL_NONE);
appearance.setPolygonAttributes(polygonAttributes);

…a jednak nějak zajistit, že normálové vektory budou orientovány oběma směry. To uděláme pomocí volání metody setBackFaceNormalFlip(boolean backFaceFlip) definované ve třídě PolygonAttributes, které způsobí, že pro zadní stranu trojúhelníku bude použit vektor opačný k normálovému vektoru přední strany. Je však pravda, že toto řešení je náročnější na výkon.

Jak ale postupovat u hladkých těles? Například u koule nebo jiných jednoduchých těles můžeme normálové vektory určit ze znalosti jejich vlastností, například u zmiňované koule tak, že víme, že v každém bodě směřují normálové vektory do jejího středu, jinde nám může pomoci analýza. Ale i tehdy, pokud nemáme přesné matematické vyjádření zobrazovaného tělesa, můžeme vytvořit hladký povrch, a to poměrně jednoduše. (Navíc dále popsaný postup lze pochopitelně použít i u matematicky snadno popsatelných těles.)

Zmíněným postupem je využití váženého součtu normálových vektorů jednotlivých trojúhelníků sousedících s vrcholem, v němž normálový vektor počítáme, přičemž váha jednotlivých normálových vektorů bude dána obsahem daných trojúhelníků. Vzhledem k tomu, že velikost vektoru vzniklého z vektorového součinu dvou vektorů se rovná dvojnásobku obsahu trojúhelníku určeného těmito vektory, stačí sečíst normálové vektory z jednotlivých trojúhelníků, které vytvoříme postupem popsaným dříve, a pak výsledek normalizovat. Tento postup se dá samozřejmě různě vylepšovat (například zadáním určitého mezního úhlu mezi trojúhelníky, při jehož překročení se už nebudeme snažit vytvářet dojem hladkého přechodu), ale to už záleží na konkrétních podmínkách.

Normálové vektory v Javě 3D

Jak už jsme si řekli minule, jsou normálové vektory stejně jako souřadnice vrcholů a jejich barvy uloženy v objektech Geometry. Ke každému vrcholu přísluší jeden normálový vektor. Normálové vektory zadáváme některou z následujících metod definovaných ve třídě GeometryArray.

• public void setNormal(int index, float[] normal)
• public void setNormal(int index, Vector3f normal)
• public void setNormals(int index, float[] normals)
• public void setNormals(int index, Vector3f[] normals)

Abychom mohli pohodlně pracovat s normálovými vektory, bude se nám ještě hodit seznámit se se třídou Vector3f a některými jejími metodami. Objekty Vector3f jsou vektory se třemi souřadnicemi reprezentovanými čísly typu float. Třída Vector3f je odvozena od třídy Tuple3f.

Ve třídě Vector3f, resp. v její nadtřídě Tuple3f, jsou definovány prakticky všechny operace, které budeme v tuto chvíli při práci s vektory potřebovat. Je to jednak metoda void add(Tuple3f t), která přičte k danému objektu objekt předaný jako parametr, metoda void sub(Tuple3f t), která slouží pro odčítání. Z metod definovaných ve třídě Vector3f to jsou metody void cross(Vector3f v1, Vector3f v2), což je vektorový součin vektorů v1 a v2 v tomto pořadí, dále například metoda dot(Vector3f), což je skalární součin, nebo metoda normalize(), která nastaví velikost tohoto vektoru na hodnotu jedna.

S těmito informacemi jsme již schopni vytvořit objekty, které bude možné osvětlovat. Jako první upravíme čtyřstěn z minulého článku, tzn. přidáme mu normálové vektory.

package interval.j3d;
import javax.media.j3d.*;
import javax.vecmath.*;
public class Ctyrsten2 extends Shape3D{
 
  float s6 = (float)Math.sqrt(6);
  float s3 = (float)Math.sqrt(3);
 
  float souradnice[] = {
   -0.5f,0,-s3/6f, 0.5f,0,-s3/6f, 0,0,s3/3f,
   0,0,s3/3f, 0,s6/3f,0, -0.5f,0,-s3/6f,
   0.5f,0,-s3/6f, 0,s6/3f,0, 0,0,s3/3f,
   -0.5f,0,-s3/6f, 0,s6/3f,0, 0.5f,0,-s3/6f};
   
  public Ctyrsten2(float hrana) {
   for (int i = 0; i < 36; i++)
    souradnice[i] *= hrana;
   setGeometry(vytvorGeometry());
   setAppearance(vytvorAppearance());
  }
  Geometry vytvorGeometry(){
   TriangleArray ta = new TriangleArray(12, GeometryArray.COORDINATES | GeometryArray.NORMALS);
   ta.setCoordinates(0,souradnice);
   for (int i = 0; i < 4; i++){
    //vektory dané hranami čtyřstěnu
    Vector3f v1 = new Vector3f(souradnice[9*i+3]-souradnice[9*i], souradnice[9*i+4]-souradnice[9*i+1], souradnice[9*i+5]-souradnice[9*i+2]);
    Vector3f v2 = new Vector3f(souradnice[9*i+6]-souradnice[9*i], souradnice[9*i+7]-souradnice[9*i+1], souradnice[9*i+8]-souradnice[9*i+2]);
    Vector3f v3 = new Vector3f();
    //získané vektory vektorově vynásobíme, čímž získáme normálový vektor
    v3.cross(v1, v2);
    //normálový vektor ještě znormalizujeme
    v3.normalize();
    // vždy třem bodům v jedné stěně nastavíme jejich normálový vektor
    for (int j = 0; j < 3; j++)
      ta.setNormal(3*i+j, v3);
   }
   return ta;
  }
  //v této metodě vytvoříme objekt Appearance
  Appearance vytvorAppearance(){
   Appearance app = new Appearance();
   Color3f ambient = new Color3f(0.5f, 0.5f, 0.5f);
   Color3f emissive = new Color3f(0,0,0);
   Color3f diffuse = new Color3f(0.9f, 0.9f, 0.3f);
   Color3f specular = new Color3f(1,1,1);
   Material material = new Material(ambient, emissive, diffuse, specular, 128);
   app.setMaterial(material);
   return app;
  }
}

V tomto příkladu jsme počítali celkem čtyři normálové vektory. Každý z nich jsme potom přiřadili třem vrcholům jedné stěny. Výsledkem je při osvětlení bodovým světlem následující obrázek.

V dalším příkladu si ukážeme, jak se vypořádat s oblými plochami. K tomu využijeme již popsaný postup spočívající v počítání váženého součtu normálových vektorů jednotlivých trojúhelníků obsahujících daný vrchol. Půjde o vytvoření objektu sloužícího k zobrazování tzv. „heightmaps“, což jsou dvojrozměrná pole, v nichž uložené hodnoty reprezentují „výšku“ bodu na daných souřadnicích.

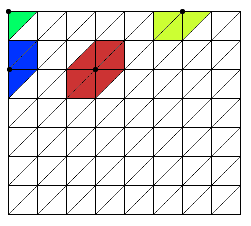
Z obrázku je vidět, že každý vrchol neležící na okraji je obsažen v šesti trojúhelnících, tzn. vážený součet budeme počítat z normálových vektorů těchto šesti trojúhelníků. (Vrcholy ležící na okrajích ošetříme v kódu zvlášť.)

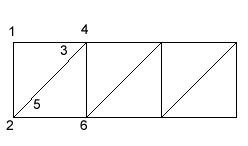
Vrcholy budeme nastavovat tak, aby šly proti chodu hodinových ručiček, v následujícím pořadí.

Zdrojový kód je kvůli své délce umístěn na zvláštní stránce.

Použijeme-li jako vstupní data pro náš objekt HeightMap funkci z = cos(x)+cos(y), bude výsledek následovný.

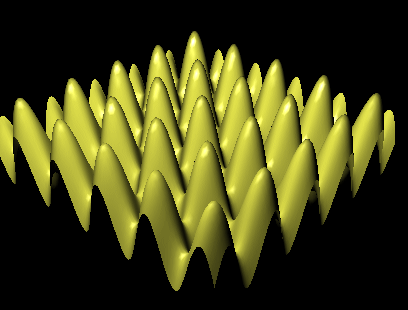
Přestože postupy popsané v tomto článku fungují, je potřeba podotknout, že se seznámíme s ještě úspornějšími způsoby, jak definovat trojúhelníkovou síť (pomocí trojúhelníkových trsů a pásů a pomocí indexované geometrie). Rovněž si v budoucnu povíme něco o třídách GeometryInfo, NormalGenerator a dalších, které by byly schopné udělat většinu toho, co jsme si dnes ukázali, za nás. Občas je ale užitečné vědět, jak můžeme normálové vektory vytvořit sami.

Starší komentáře ke článku

Pokud máte zájem o starší komentáře k tomuto článku, naleznete je zde.