Java a 3D grafika – Geometry (GeometryStripArray)
Vrcholy těles, která jsme vytvořili v předchozím článku, nebyly sdíleny mezi jednotlivými trojúhelníky, přestože se trojúhelníky vzájemně dotýkaly. Z hlediska nároků na paměť je takový způsob uložení poměrně neefektivní. V tomto článku se seznámíme se třídami pro vytváření trojúhelníkových trsů a pásů, jejichž využití tento problém zčásti řeší. V druhé části článku pak trochu odbočíme a ukážeme si jeden docela zajímavý algoritmus pro generování „krajin“.
Na následujícím obrázku je zobrazen příklad trsu trojúhelníků a pásu trojúhelníků. Čísla v obrázku udávají pořadí, v jakém do těchto objektů vkládáme vrcholy.
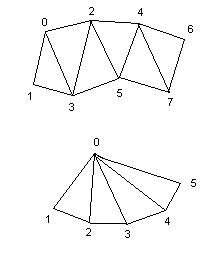
Třídy pro práci s trsy a pásy jsou všechny odvozeny od abstraktní třídy GeometryStripArray, která je odvozena od třídy GeometryArray. V této třídě je definován konstruktor, s nímž budeme v tomto článku pracovat, a to GeometryStripArray(int vtxCount, int vertexFormat, int stripVertexCount[]). Tento konstruktor přebírá tři parametry. První z nich, vtxCount, určuje celkový počet vrcholů, které budou uloženy v tomto objektu, druhý parametr má stejný význam jako u konstruktoru třídy GeometryArray a určuje tedy, co všechno bude v tomto objektu uloženo (souřadnice vrcholů, barvy, normálové vektory a další). Posledním parametrem je pole čísel typu int, která udávají počet vrcholů v jednotlivých pásech, popřípadě trsech, protože do objektu GeometryStripArray jich můžeme uložit i více.
Pro nastavování vrcholů, barev a pro ostatní činnosti, jako je například dotazování se „getter“ metodami, se používají metody definované ve třídě GeometryArray, s níž jsme se již seznámili.
Nyní můžeme přejít k prvnímu příkladu, jímž bude vytvoření šroubové plochy pomocí pásu trojúhelníků. Pásy trojúhelníků se v Javě 3D vytvářejí pomocí instancí třídy TriangleStripArray. Náš program, který vytváří šroubovou plochu, není příliš efektivní kvůli příliš velkému počtu volání funkcí sinus a kosinus. Tato volání by šla nahradit použitím rotace o konstantní úhel, ale kvůli čitelnosti jsem je ponechal v tomto tvaru.
int vertexCounts[] = {300};
TriangleStripArray tsa = new TriangleStripArray(300, GeometryArray.COORDINATES | GeometryArray.NORMALS, vertexCounts);
float r = 0.5f;
for (int i = 0; i < 300; i+=2){
float x = r*(float)Math.cos(i/20f);
float y = r*(float)Math.sin(i/20f);
float z = i/300f;
tsa.setCoordinate(i, new Point3f(0, 0, z));
tsa.setCoordinate(i+1, new Point3f(x, y, z));
}
Zdrojový kód zde neuvádím celý, protože k vypočítání normálových vektorů je v něm použita třída NormalGenerator, s níž jsme se ještě nesetkali.
V dalším příkladu vytvoříme pro změnu kuželovou plochu pomocí trsu trojúhelníků. Pro vytváření trsů trojúhelníků budeme potřebovat třídu TriangleFanArray. Pro efektivitu tohoto programu platí totéž, co jsme si řekli u předchozího programu.
int vertexCount[] = {32};
TriangleFanArray tfa = new TriangleFanArray(32, GeometryArray.COORDINATES | GeometryArray.NORMALS, vertexCount);
tfa.setCoordinate(0, new Point3f(0,0,1));
float r = 0.5f;
for (int i = 1; i < 32; i++){
float x = r*(float)Math.cos(Math.PI*i/15f);
float y = r*(float)Math.sin(Math.PI*i/15f);
tfa.setCoordinate(i, new Point3f(x,y,0));
}
To je zatím vše, co se týče tříd odvozených od třídy GeometryArray. Příště se začneme zabývat indexovanou geometrií. Nyní se podíváme na jeden docela zajímavý algoritmus pro generování terénů.
Generování terénů
Pro generování terénů existuje celá řada algoritmů, z nichž asi nejpopulárnější jsou ty využívající fraktály (pokud vás tato problematika zajímá, tak na Rootu vyšel článek o mid-point displacement algoritmu). My se v tomto článku nebudeme zabývat žádným algoritmem využívajícím fraktály, ale ukážeme si modifikaci „kopečkového“ algoritmu popsanou na robot frog.
Základní myšlenka tohoto algoritmu je velice prostá. Na náhodně vybraná místa umístíme kopečky s náhodnými velikostmi. Při dostatečně velkém množství kopečků začne náš terén připomínat skutečnou krajinu, byť ne tak realistickou, jako bychom získali při použití nějakého algoritmu využívajícího fraktálů, ale i to může být mnohdy přínosem.
V programu to uděláme následovně. Začneme s height-mapou, jejíž výšky nastavíme na nulu. Náhodně vybereme bod ležící na naší ploše, což bude střed kopečku, a k němu náhodně vybereme další číslo – poloměr. Ke každému bodu uvnitř kruhu daného poloměrem a středem přičteme hodnotu poloměr*poloměr - (k-x)*(k-x) - (j-y)*(j-y), což je vzorec pro rotační paraboloid „překlopený směrem dolů“. Tento postup zopakujeme, kolikrát budeme chtít. Potom celý terén posuneme, aby jeho nejnižší bod měl z-ovou souřadnici rovnou nule. Dále vynásobíme všechny body hodnotou 1/(max-min), díky čemuž budou všechny výšky v intervalu od 0 do 1. Výšky všech bodů potom můžeme umocnit na druhou. Tento krok sice není nezbytný, jeho využitím ale můžeme získat krajinu s hezkými údolíčky. Nakonec všechny výšky vynásobíme parametrem maxVyska, udávajícím maximální výšku našeho terénu. Zdrojový kód, který toto všechno dělá, je na následujícím výpisu:
package interval.j3d;
import java.util.Random;
public class Hills {
// vytvářet tuto třídu by mohlo být zbytečné
private Hills() {
}
//tato metoda nám naplní pole data hodnotami odpovídajícími
//výškám jednotlivých bodů v našem terénu
public static void generateTerrain(float data[][], int minPolomer, int maxPolomer, int pocetIteraci, float maxVyska){
int rozmerY = data.length;
int rozmerX = data[0].length;
float max = 0;
float min = 0;
//vytvoříme generátor náhodných čísel
Random rand = new Random(System.currentTimeMillis());
//tato smyčka provádí postup, který jsme si popsali v článku
for (int i = 0; i < pocetIteraci; i++){
//vybereme souřadnice středu nového kopečku…
int x = rand.nextInt(rozmerX);
int y = rand.nextInt(rozmerY);
//… a poloměr
int polomer = minPolomer + rand.nextInt(maxPolomer-minPolomer+1);
int j0, k0, maxJ, maxK;
//dále se musíme vypořádat s body, které sice jsou na kladné části
//rotačního paraboloidu (kopečku), ale leží mimo stanovené hodnoty x,y
if (y-polomer >= 0)
j0 = y-polomer;
else
j0 = 0;
if (y+polomer < rozmerY)
maxJ = y+polomer;
else
maxJ = rozmerY;
if (x-polomer >= 0)
k0 = x-polomer;
else
k0 = 0;
if (x+polomer < rozmerX)
maxK = x+polomer;
else
maxK = rozmerX;
//v těchto cyklech vytváříme naše kopečky
//přičtením hodnoty polomer*polomer – (k-x)*(k-x) – (j-y)*(j-y)
//k číslu na data[j][k]
for (int j = j0; j < maxJ; j++){
for (int k = k0; k < maxK; k++){
float z = polomer*polomer – (k-x)*(k-x) – (j-y)*(j-y);
if (z > 0){
data[j][k] += z;
max = Math.max(data[j][k], max);
min = Math.min(data[j][k], min);
}
}
}
}
//musíme upravit výšku, aby byla v rozumných mezích
scale(data, min, max, maxVyska);
}
protected static void scale(float data[][], float min, float max, float vyska){System.out.println(min+“ „+max);
for (int i = 0; i < data.length; i++){
for (int j = 0; j < data[0].length; j++){
data[i][j] -= min;
data[i][j] *= (1/(max-min));
data[i][j] *= data[i][j];
data[i][j] *= vyska;
}
}
}
}
Objekt Shape3D, obsahující náš terén, pak vytvoříme snadno s využitím třídy HeightMap z předchozího článku, jak můžeme vidět dále. (Třídu HeightMap lze snadno upravit tak, aby používala pásy trojúhelníků.)
float heights[][] = new float[170][170];
Hills.generateTerrain(heights, 0, 20, 800, 0.3f);
HeightMap hm = new HeightMap(heights, 1.2f, 1.2f);
Pokud nastavíme příliš malý počet iterací, nebude náš terén vypadat vůbec reálně. S velkou pravděpodobností to bude pouze několik osamocených částí rotačních paraboloidů trčících z roviny. Přesvědčit se o tom můžeme na následujícím obrázku, který byl vytvořen s počtem iterací rovným deseti:
Další obrázek už ukazuje terén, u něhož jsme počet iterací nastavili na mnohem větší hodnotu, konkrétně 800:
Poslední obrázek ještě ukazuje, jak by vypadal terén, pokud bychom výšky nejprve neumocnili. Záleží samozřejmě jen na vás, kterou variantu si zvolíte.
Tento algoritmus je pochopitelně možné různě obměňovat. Například můžeme změnit funkci generující kopečky. Taktéž můžeme náhodně jednou vytvořit kopeček a jindy zase údolí. Změnit se dá také rozložení náhodných čísel, například je možné použít gaussovské rozložení. Zkrátka, možností je nepřeberně.
