Java – pokročilá grafika (Shape, Path, Area)

V tomto článku ze série o pokročilé grafice v Javě se budeme zabývat prací s geometrickými objekty. Dojde i na slibované cesty a oblasti.

Shape

Nejdříve ze všeho se ale musíme blíže seznámit s rozhraním Shape, které je implementováno všemi třídami reprezentujícími geometrické objekty, tedy i třídou GeneralPath, reprezentující cestu. K metodám tohoto rozhraní se již nebudu dále příliš vracet. Jejich účel je ve všech třídách, které ho implementují, stejný. Rozhraní Shape definuje následující metody:

boolean contains(double x, double y)
  boolean contains(double x, double y, double w, double h)
  boolean contains(Point2D p)
  boolean contains(Rectangle2D r)
  Rectangle getBounds()
  Rectangle2D getBounds2D()
PathIterator getPathIterator(AffineTransform at)
  PathIterator getPathIterator(AffineTransform at, double flatness)
  boolean intersects(double x, double y, double w, double h)
  boolean intersects(Rectangle2D r)

Varianty metody contains zjišťují, zda bod (1. a 3. varianta) nebo obdélník (2. a 4. varianta) leží uvnitř objektu, ze kterého jsou volány.

Metody getBounds a getBounds2D vracejí obdélník uzavírající daný objekt, přičemž metoda getBounds2D pracuje s proměnnými typu double a vrací obdélník Rectangle2D, zatímco metoda getBounds pracuje pouze s proměnnými typu int a vrací obdélník Rectangle.

Dvě varianty metody getPathIterator vracejí instanci třídy implementující rozhraní PathIterator. PathIterator obsahuje metody, kterými „říká“, jak má být tvar vykreslován (teď rovná čára, teď parabola atd.). Tímto rozhraním se ještě možná budeme zabývat v některém z dalších článků. Nyní pro nás ale metoda getPathIterator není nijak významná a nebudeme se jí dále zabývat.

Metoda intersects zjišťuje, zda daný objekt protíná obdélník, zadaný buď souřadnicemi levého horního rohu a šířkou a výškou, nebo objektem Rectangle2D. Že se protínají, znamená, že mají alespoň jeden bod společný. Tato metoda ale nemusí být stoprocentně spolehlivá, protože, jak se uvádí v dokumentaci, pokud by byl přesný výpočet příliš náročný, může se provést pouze přibližný.

Třídy pro kreslení geometrických tvarů

Velice užitečnými metodami, které obsahuje třída Graphics2D, jsou metody draw(Shape s) a fill(Shape s). Metoda draw vykresluje objekt Shape a metoda fill objekt Shape pro změnu vyplňuje. Konstruktory některých tříd implementující rozhraní Shape jsou: Rectangle2D.Double(double x, double y, double w, double h), Ellipse2D.Double(double x, double y, double w, double h), Line2D.Double(double x1, double y1, souble x2, double y2), CubicCurve2D.Double(x1, y1, ctrlx1, ctrly1, ctrlx2, ctrly2, x2, y2) (Beziérova křivka), QuadCurve2D.Double(x1, y1, ctrlx1, ctrly1, x2, y2) (parabola)… Parametry x, y u konstruktorů elips a obdélníků jsou souřadnice levého horního rohu, parametry w a h udávají šířku a výšku. Parametry ctrlx1, ctrly1, ctrlx2, ctrly2 jsou souřadnice řídících bodů křivek.

Jako ukázku uvádím vykreslení Beziérovy křivky, k čemuž bylo před příchodem javy 2D nutné vytvořit vlastní implementaci s použitím vzorců a metody Polyline.

import java.awt.*;
import java.awt.geom..*;
//…
public void paint (Graphics g) {
  Graphics2D g2 = (Graphics2D)g;
  Shape c = new new CubicCurve2D.Double(0,0,0,50,100,50,100,100);
g2.draw(c);
}
//…

A teď si představte, že chcete vykreslovanou křivku převrátit podle svislé osy a zúžit ji na polovinu. Vzpomínáte si ještě, co bylo tématem minulého dílu? Ano, použijeme transformace pomocí třídy AffineTransform. Převrácení a zároveň zúžení dosáhneme zavoláním metody scale s parametrem sx = -0.5 a sy = 1. Tím ale transformace nekončí, protože křivka, kterou jsme vytvořili, se vlivem transformace dostala mimo viditelnou oblast okna, takže ji musíme posunout zase zpět, ale jakoby na opačnou stranu (znaménko mínus v příkladu), protože nesmíme zapomínat na to, že jsme objektu AffineTransform změnili jeho souřadnou soustavu. Popřípadě bychom mohli křivku transformovat dvakrát a před druhým transformováním volat metodu setToTranslation místo metody translate.

//…
public void paint (Graphics g) {
  Graphics2D g2 = (Graphics2D)g;
  AffineTransform af = new AffineTransform();
  af.scale(-0.5,1);
    af.translate(-100,0);
Shape c = new CubicCurve2D.Double(0,0,0,50,100,50,100,100);
  c = af.createTransformedShape(c);
g2.draw(c);
}
//…

Cesty

Dost již ale bylo transformací, nyní se podíváme konečně na třídu GeneralPath. A začneme hned příkladem:

import java.awt.*;
import java.awt.geom.*;
import javax.swing.*;
public class Pokus1 extends JApplet {
GeneralPath gp = new GeneralPath();
GeneralPath gp2 = new GeneralPath();
//…
public void init() {
// první tvar
gp.moveTo(10,10);
gp.curveTo(5,20,200,40,5,70);
gp.curveTo(300,100,400,60,10,10);
// druhý tvar
gp2.moveTo(100,100);
    gp2.quadTo(200,300,300,100);
gp2.closePath();
}
public void paint (Graphics g) {
Graphics2D g2 = (Graphics2D)g;
    g2.setColor(Color.blue);
    g2.fill(gp);
    g2.setColor(Color.green);
    g2.fill(gp2);
}}

A toto je výsledek několika řádek kódu z příkladu. Snadné, ačkoliv ne zrovna nejvkusnější:

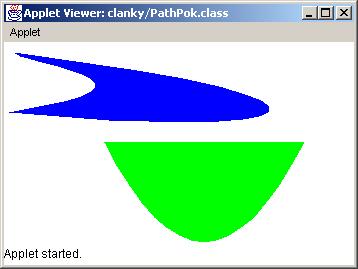
Jak jsme postupovali? Na začátku jsme vytvořili dvě instance třídy GeneralPath. V metodě init jsme do nich potom nakreslili požadované tvary. První tvar jsme vytvořili pomocí dvou Beziérových křivek, druhý potom pomocí paraboly a uzavírající úsečky. Při vytváření cest se musí vždy nejprve cesta inicializovat voláním metody moveTo, které se jako parametry předávají souřadnice počátečního bodu.

Přidávat úsečky a křivky můžeme v podstatě dvěma způsoby, voláním metod lineTo, curveTo, quadTo, jako jsme to udělali v našem příkladu, nebo voláním metody append(Shape s, boolean connect). Prvně jmenovaný způsob použijete, pokud budete chtít stále jen připojovat další čáry. Parametry těchto metod jsou stejné jako parametry konstruktorů grafických objektů, které chceme kreslit, s tím rozdílem, že chybí první řídící bod, který je nahrazen posledním bodem cesty.

Metoda append umožňuje přidávat nejen čáry, ale i obdélníky, elipsy a podobně. Parametrem connect říkáme této metodě, zda chceme, aby spojila tento objekt čarou s posledním bodem cesty.

Sice je toho mnoho, co lze s cestami dokázat, ale stále to ještě není ono, že? Tak se podívejme na další třídu z balíku java.awt.geom, na třídu Area.

Area

Třída Area je další ze tříd pro práci s geometrickými objekty, přesněji řečeno s uzavřenými oblastmi. Na rozdíl od tříd, kterými jsme se již zabývali, poskytuje operace jako je průnik, logická operace XOR atd. Abych vás neumořil další sprškou referenčních údajů, podíváme se hned na příklad, ke kterému budeme potřebovat pouze konstruktor a metodu intersect (průnik). Konstruktor, se kterým budeme pracovat, má jen jediný parametr, kterým je objekt Shape. Metoda intersect je typu void a předává se jí rovněž objekt Shape.

Teď již k příkladu. Chceme vytvořit grafickou komponentu, ve které budou létat dvě elipsy odrážející se od okrajů. Tyto elipsy nebudou vybarvené, vybarvený bude pouze jejich průnik.

package tvary;
import java.util.*;
import java.awt.*;
import java.awt.geom.*;
import javax.swing.*;
import java.awt.event.*;
public class Animovadlo extends JComponent{
  Ellipse2D.Double s1, s2;
  Area a1, a2, a;
  double vx1, vy1, vx2, vy2//x-ové a y-ové složky rychlostí elips
  double vmax=10, w=60, h=60;
  int width = 200, height = 200;
  boolean not_end = true;
  public Animovadlo () {
    this.addComponentListener(new ComponentAdapter() {
     public void componentResized(ComponentEvent event){
      width = getWidth();
      height = getHeight();
     }
    }
    );
    double x1, y1, x2, y2;
// nastavení náhodných hodnot
    Random r = new Random(new Date().getTime());
    x1 = Math.abs(r.nextInt()%(width-w));
    x2 = Math.abs(r.nextInt()%(width-w));
    y1 = Math.abs(r.nextInt()%(height-h));
    y2 = Math.abs(r.nextInt()%(height-h));
    vx1 = Math.abs(r.nextInt()%vmax);
    vx2 = Math.abs(r.nextInt()%vmax);
    vy1 = Math.abs(r.nextInt()%vmax);
    vy2 = Math.abs(r.nextInt()%vmax);
    s1 = new Ellipse2D.Double(x1,y1, w, h);
    s2 = new Ellipse2D.Double(x2, y2, w, h);
    a1 = new Area(s1);
    a2 = new Area(s2);
// postačí anonymní třída
    Thread t = new Thread(new Runnable() {
    public void run(){
     while (not_end){
// posunutí elips
      s1.x += vx1;
      s1.y += vy1;
      s2.x += vx2;
      s2.y += vy2;
// zjištění, jestli se už má elipsa odrazit od okraje
      if (s1.x+s1.width > width){
      s1.x = width-s1.width;
      vx1 *= -1;
      }
      if (s1.x < 0){
      s1.x = 0;
      vx1 *= -1;
      }
      if (s1.y+s1.height > height){
      s1.y = height-s1.height;
      vy1 *= -1;
      }
      if (s1.y < 0){
      s1.y = 0;
      vy1 *= -1;
      }
      if (s2.x+s2.width > width){
      s2.x = width-s2.width;
      vx2 *= -1;
      }
      if (s2.x < 0){
      s2.x = 0;
      vx2 *= -1;
      }
      if (s2.y+s2.height > height){
      s2.y = height-s2.height;
      vy2 *= -1;
      }
      if (s2.y < 0){
      s2.y = 0;
      vy2 *= -1;
      }
// vytvoření oblastí z elips
      a1 = new Area(s1);
      a2 = new Area(s2);
// na první elipsu použijeme průnik s druhou
      a1.intersect(a2);
// překreslíme komponentu
      repaint();
      try {
      Thread.sleep(100);
      } catch (InterruptedException e) {
      System.out.println(e);
      }
     }
    }});
  t.start();
  }
  public void paintComponent(Graphics g) {
    Graphics2D g2 = (Graphics2D)g;
    g2.setColor(Color.white);
    g2.fillRect(0,0,getWidth(),getHeight());
    g2.setColor(Color.black);
    g2.drawRect(0,0,width-1,height-1);
// vykreslení hranic elipsy
    g2.draw(s1);
    g2.draw(s2);
// vyplnění průniku elips
    g2.fill(a1);
  }
  public Dimension getMaximumSize(){
    return new Dimension(width, height);
  }
  public Dimension getPreferredSize(){
    return new Dimension(width,height);
  }
  public Dimension getMinimumSize(){
    return new Dimension(width,height);
  }
}

Kód apletu, který bude zobrazovat naše „létající elipsy“, bude potom vypadat jenom takto:

package tvary;
public class Pruniky extends javax.swing.JApplet {
  Animovadlo a = new Animovadlo();
  public Pruniky() {
    getContentPane().add(a);
  }
}

Doufám, že vás tento příklad navnadil k přečtení dalšího dílu této série článků, ve kterém se ke třídě Area ještě vrátíme a ve které si konečně ukážeme práci s různými typy čar a vyplnění.