Java – pokročilá grafika pro všechny

Následující série článků vás seznámí s možnostmi, které Java skýtá v oblasti grafiky. Ukážeme si, jak dosáhnout zajímavých efektů s minimálním úsilím. Seznámíme se s třídami pro práci s grafikou, s cestami i na třídy, které mají na starost vykreslování čar a vyplněných oblastí.

Graphics versus Graphics2D

Dejme tomu, že chceme s použitím třídy Graphics vytvořit třídu, která bude vykreslovat jednoduchý domeček. Následující výpis ukazuje její kód:

import java.awt.*;
public class Domecek {
  protected int xx, yy, w, h;
  public Domecek(int x, int y, int width, int height){
     xx = x;
     yy = y;
     w = width;
     h = height;
}
  public void move (int deltax, int deltay){
//…
}
  public void resize(int width, int height) {
//…
}
  public void draw(Graphics g) {
  g.drawRect(xx,yy,w,h);
  g.drawLine(xx,yy,xx+w/2,yy-h/2);
  g.drawLine(xx+w/2,yy-h/2,xx+w,yy);
  }
}

Běžnou operací v grafických editorech je otočení objektu. Takto vytvořený domeček však neotočíme ani s použitím vzorců pro rotaci, protože používá metodu drawRect. A drawRect při používání třídy Graphics neotočíte. Jaké tedy máme možnosti? Přepsat třídu Domecek, aby používala metody drawPolygon a drawPolyline, a implementovat do ní metody pro otáčení? Ne. Řešení, ke kterému směřuji, je mnohem jednodušší. Jedná se o použití třídy Graphics2D, odvozené od třídy Graphics, a její metody rotate(double angle, double x, double y), kde angle je úhel otočení v radiánech a x a y jsou souřadnice bodu, kolem kterého má dojít k otočení. Její použití při otočení domečku je následující:

//…
public void paint(Graphics g) {
//metodě paint je v současných běhových prostředích
//předáván parametr typu Graphics2D
Graphics2D g2 = (Graphics2D)g;
g2.rotate(Math.PI/4,20,20); //otočíme všechno, co bude kresleno po volání rotate
new Domecek(20,20,10,10).draw(g2);
}
//…

Pravděpodobně nepoužijete metodu rotate k otáčení domečků, ale může se vám velmi hodit, pokud budete chtít otáčet například text.

Jinou metodou pro změnu soustavy souřadné je metoda translate, která posunuje její počátek. Existuje ve dvou verzích lišících se typem argumentů. První (zděděná ze třídy Graphics) je translate(int x, int y), která posunuje počátek na pozici danou souřadnicemi x a y, druhou verzí je translate(double tx, double ty).

Je potřeba si uvědomit, že k posunu (i jiné transformaci) se používají souřadnice již transformované, tzn. jestliže jsme již použili metodu rotate a posuneme nyní soustavu souřadnou například o hodnotu 10 na ose x, dojde k posunutí i vůči fyzické ose y a posunutí vůči fyzické ose x bude jiné, než zadaných 10 (pokud jsme samozřejmě neotočili soustavu o násobek 2π).

Další metodou je metoda scale(double sx, double sy), pomocí níž můžete měnit měřítko os. Hodnota větší než 0 a menší než 1 způsobí zmenšení, zatímco hodnota větší než 1 zvětšení. Poslední ze čtveřice metod pro transformace je shear(double sx, double sy). Tato metoda je trochu méně intuitivní než předešlé. Posunuje totiž x-ové souřadnice o hodnotu sx*y a y-ové o sy*x.

AffineTransform

Přestože je práce s uvedenými metodami vcelku pohodlná, nabízí Java ještě lepší možnost, jak transformovat soustavu souřadnou (a nejen ji). Tou možností je používání třídy AffineTransform z balíku java.awt.geom (tzn. pokud ji chcete používat, musíte uvést v importu tento balík), kterou si můžeme představit jako čtvercovou matici o devíti prvcích.

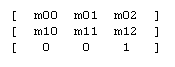
Pokud provádíme operace s třídou AffineTransform, násobíme vlastně matice. Jako příklad uvedu použití matice pro posunutí:

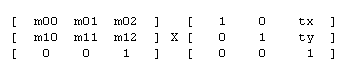
Vytvořit instanci třídy AffineTransform můžete například pomocí bezparametrového konstruktoru AffineTransform(), který vytváří matici identity (nedojde k žádné změně při jejím použití), konstruktoru AffineTransform(float m00, float m10, float m01, float m11, float m02,float m12) nebo konstruktoru AffineTransform(float[] flatmatrix), kde flatmatrix je pole buď o čtyřech prvcích, které reprezentují hodnoty m00 m10 m01 m11, nebo o šesti prvcích, které reprezentují hodnoty všech prvků horních dvou řádek. Tyto konstruktory existují i ve verzi pro proměnné typu double.

Třída AffineTransform obsahuje stejné metody jako ty, které jsme si předvedli u třídy Graphics2D, s výjimkou metody translate(int x, int y). Nebudu se zde samozřejmě rozepisovat o všech metodách této třídy. Pokud vás zajímají, podívejte se na dokumentaci na Sunu. Jako zajímavé se mohou jevit metody setToIdentity() (nastaví matici na identitu, tedy jakoby ji „vynuluje“), setToTranslation(double tx, double ty), setToRotation(double angle, double x, double y) a setToScale(double sx, double sy), jejichž činnost si můžeme představit jako volání metody setToIdentity a příslušné další metody (např rotate nebo translate).

Použití třídy AffineTransform si ukážeme na příkladu našeho domečku:

import java.awt.*;
import java.awt.geom..*;
//…
public void paint(Graphics g) {
    Graphics2D g2 = (Graphics2D)g;
    AffineTransform af = new AffineTransform();
    af.translate(400,100);
    af.rotate(Math.PI/4);
    af.scale(0.5,1);
    g2.setTransform(af);
    new Domecek(-25,-25,50,50).draw(g);
}
//…

Co jsme si zatím ukázali, však není ani zdaleka vše, co třída AffineTransform nabízí. Z dalších užitečných metod jmenuji například metodu createInverse(), která vrací instanci třídy AffineTransform inverzní k původní. Že je inverzní, znamená, že použijeme-li transformaci původní a inverzní maticí, nestane se nic, protože se jejich účinky vyruší. Jinými slovy – pokud původní matice posunuje počátek o hodnotu 100, vrací ji inverzní matice zase zpět, tedy posunuje ji o –100. Pokud se stane, že inverzní matice neexistuje (determinant je roven nule), dojde k vyvolání výjimky NoninvertibleTransformException.

Metoda transform(Point2D[] ptSrc,int srcOff,Point2D[] ptDst, int dstOff, int numPts) transformuje body z pole ptSrc a ukládá je do pole ptDst, přičemž začátek bodů, které mají být transformovány, je ptSrc[srcOff], začátek transformovaných bodů se uloží na ptDst[dstOff] a počet transformovaných bodů je numPts. Rovněž existuje metoda pro transformaci bodů inverzní maticí, a to inverseTransform, jejíž volání je stejné jako u metody transform. Podobnou funkci jako předešlé metody má deltaTransform(Point2D[] ptSrc,int srcOff,Point2D[] ptDst, int dstOff, int numPts), s tím rozdílem, že považuje body za vektory, což znamená, že na ně nepoužívá složku pro posunutí. Zavoláním af.concatenate(AffineTransform c) transformujeme AffineTransform af pomocí AffineTransform c.

Jinou užitečnou metodou je createTransformedShape(Shape pSrc), která vrací odkaz na instanci třídy, která implementuje rozhraní Shape. Třídy, které toto rozhraní implementují, reprezentují nějaký geometrický tvar, se kterým je možné provádět určité operace. Až si v příštím článku povíme něco o cestách, vrátíme se k této metodě.

Starší komentáře ke článku

Pokud máte zájem o starší komentáře k tomuto článku, naleznete je zde.